Fundamentos básicos de hidráulica (4 de 5)
- Miguel Angel Monge

- 21 mar 2021
- 5 Min. de lectura
Actualizado: 21 nov 2021
DEL CAUDAL, LA PRESIÓN Y LA VELOCIDAD DEL AGUA
A veces se confunde la relación que existe entre la presión y la velocidad del agua en el interior de una conducción. A igualdad de diámetro de un tubo que transporta agua, cuando aumenta su velocidad lo que implica es un incremento del caudal, pudiéndose mantener la misma presión. Para entenderlo supongamos dos tuberías exactamente iguales (por ejemplo de 25 mm de diámetro) y al final de cada una de ellas enlazan con una línea de riego. Una tubería enlaza con una línea de 6 aspersores de 520 litros/hora de caudal cada uno y la otra tubería enlaza con una línea de 390 goteros de 4 litros/hora cada uno. Ambas líneas deben de funcionar con una presión de entrada de 2,5 bar. En el inicio de ambas líneas la presión es la misma, sin embargo las velocidades de circulación del agua en las tuberías que las alimentan serán diferentes, ya que los caudales circulantes también lo son.

En este ejemplo la tubería que suministra agua a los aspersores transporta el doble de caudal que la tubería que suministra agua a los goteros; aunque la presión en ambas tuberías sea la misma, difiere el caudal y por consiguiente la velocidad del agua. Recordemos la ecuación de continuidad que vimos en la primera entrega: Q = S · v. Un tubo transporta el doble de caudal que el otro, por tanto, como la sección es la misma, implica que la velocidad será también el doble: 2Q = S · 2v.
Supongamos un circuito con una tubería y una bomba que proporciona energía al agua con un grifo cerrado al final del tubo. La bomba transmitirá al agua una presión de 4 kg/cm2.
Si pusiéramos en funcionamiento la bomba con el grifo cerrado, la presión en cualquier punto del circuito sería de 4 kg/cm2 ya que al no haber circulación de agua no existen pérdidas de energía debidas al rozamiento. Lo enunció Pascal en la ley que lleva su nombre: “La presión ejercida sobre la superficie libre de un líquido confinado dentro de un recipiente se transmite con la misma intensidad a todo el fluido”
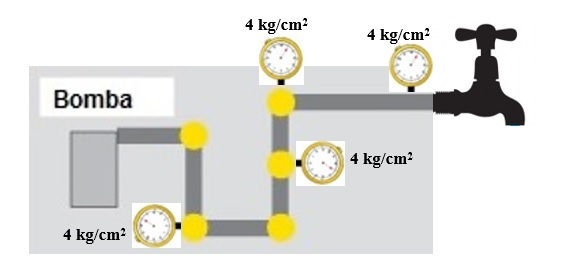
Si abriésemos el grifo totalmente, la presión a la salida de la bomba seguiría siendo evidentemente de 4 kg/cm2 pero a la entrada del grifo ya no sería de 4 kg/cm2 pues debemos de descontar las pérdidas de carga producidas en el circuito. Si estas pérdidas, para un caudal determinado, fuesen por ejemplo de 0,6 kg/cm2, entonces a la entrada del grifo tendríamos pe = 4-0,6 = 3,4 kg/cm2. Pero aún el agua tiene otra pérdida de presión ya que debe de circular por el interior del grifo. Si ésta pérdida fuese, por ejemplo, de 4 mca, la presión de salida sería de ps = 3,4-0,4 = 3 kg/cm2. Esta sería entonces la lectura que daría un manómetro de aguja en la boquilla de salida del grifo.
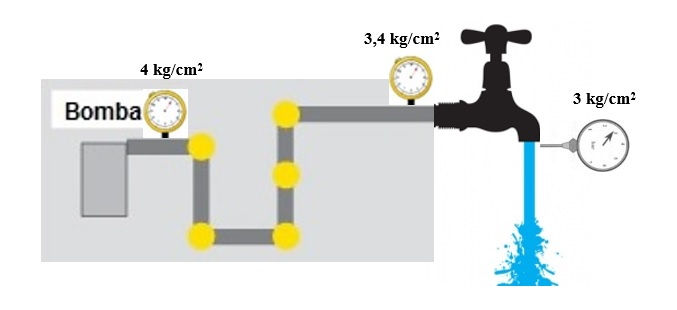
Recordemos el teorema de Bernoulli que vimos en la entrega anterior. Al encontrarnos en la misma cota podemos eliminar el término Z en la ecuación y entonces el balance energético en la conducción sería:

H son las pérdidas de carga totales (tubo y accesorios)
Como v1 = v2 entonces:
pbomba = pgrifo + H
pgrifo = pbomba – H
3 = 4 – (0,6 + 0,4)
Bien, si 3 kg/cm2 de presión a la salida del grifo no fuese suficiente para nuestro propósito, entonces tendríamos que pedir más presión al equipo de bombeo, y por consiguiente también aumentaría el caudal a la salida del grifo. La bomba impulsaría el agua a una mayor velocidad (recordemos Q = S · v)
Por el lado contrario si fuesen excesivos 3 kg de presión, cerraríamos el grifo hasta alcanzar la consigna de presión que necesitásemos, y disminuiría por tanto el caudal circulante.
En las redes hidráulicas se instalan válvulas que controlan tanto la presión como el caudal y son utilizadas para garantizar al usuario una presión mínima en su toma de servicio.
Supongamos que al circuito hidráulico anterior le agregamos una válvula reguladora. Esta válvula podría ser reductora de presión, podría ser limitadora de caudal o bien podría realizar ambas funciones, de tal forma que aguas abajo de la válvula mantuviese una presión más baja y constante que aguas arriba limitando también el caudal máximo a un valor prefijado.

¿Qué sucede en una reducción de la sección de la tubería?
Supongamos una tubería en la que existe una reducción de su sección y por la que circula un caudal determinado. El caudal que entra por un extremo del tubo es el mismo que el que sale por el otro extremo.
Si aplicamos la ecuación de continuidad en dos secciones del tubo (sección 1, la mayor y sección 2, la menor), tendremos:
S1 · v1 = S2 · v2 = constante
Como S1 es mayor que S2 se deduce que para mantener constante la igualdad entonces v1 tiene que ser menor que v2 como hemos visto al principio de este post.
Aplicando ahora Bernoulli según vimos en el post anterior, tendríamos:

Vamos a simplificar esta ecuación haciendo Z1 = Z2, ya que el tubo se encuentra a la misma cota.


¿Qué os recuerda el esquema de arriba?
El efecto Venturi consiste en que un fluido en movimiento dentro de un conducto cerrado disminuye su presión cuando aumenta la velocidad al pasar por una zona de sección menor. En ciertas condiciones, cuando el aumento de velocidad es muy grande, se llegan a producir presiones muy bajas y entonces, si en ese punto del conducto se introduce el extremo de otro conducto, se produce una aspiración del fluido que se mezclará con el que circula por el primer conducto. Este efecto, demostrado en 1797, recibe su nombre del físico italiano Giovanni Battista Venturi.
Un tubo de venturi es un dispositivo inicialmente diseñado para medir la velocidad de un fluido aprovechando el efecto venturi. Efectivamente, conociendo la velocidad antes del estrechamiento y midiendo la diferencia de presiones, se halla fácilmente la velocidad en el punto deseado.
En agricultura, el inyector venturi es el sistema de inyección de fertilizante más económico y extendido. Se compone de un pequeño dispositivo de plástico en forma de T, con un estrechamiento interior, por donde se inyecta el fertilizante en la red por diferencia de presión. Es un sistema sencillo, con muy poco mantenimiento. La inyección de fertilizante es proporcional al caudal que circula por el venturi.
La imagen siguiente muestra seccionado un inyector venturi.

Imagen de portada:
Diagrama de Venn
Los diagramas de Venn llevan el nombre del lógico británico, John Venn. Él escribió sobre ellos en un artículo redactado en 1880.
Sin embargo, las raíces de este tipo de diagrama se remontan a un período muy anterior, al menos 600 años atrás. Alrededor del año 1200, el filósofo y lógico español Ramón Llull, usó un tipo de diagrama similar.
En la década de 1700, el matemático suizo Leonard Euler inventó lo que luego se conocería como "diagrama de Euler", el predecesor más directo del diagrama de Venn.
Los diagramas de Euler-Venn se convirtieron en una parte del plan de estudio de la "nueva matemática" en la década de 1960.
¿Quién fue Pascal?
Blaise Pascal (1623 - 1662) fue un matemático, físico, filósofo y escritor francés. Sus estudios realizaron aportes a la teoría de la probabilidad, investigaciones sobre los fluidos y la aclaración de conceptos tales como la presión y el vacío.
La unidad de presión pascal (Pa) fue nombrada en su homenaje.
¿Quién fue Venturi?
Giovanni Battista Venturi (1746 - 1822) fue un físico italiano. Descubrió el efecto venturi que lleva su nombre. Fue coetáneo de Leonard Euler y de Daniel Bernoulli.
